UT-BASEがお送りする「後期課程の歩き方」(学部学科紹介)は、後期課程での学生生活を紹介しています。しかし、今この拙文をお読みいただいている好奇心旺盛・頭脳明晰・明鏡止水な読者の皆様は「どんな雰囲気かは分かったけど、具体的に何が学べるのだろう…?」とお思いのことでしょう。
そこで!!「学部学科紹介イカ東edition」つまり、後期課程の本学学生が学ぶ学問領域を"エンジン全開"で語り倒す企画を実施させていただきます!
一端の学部生が書いているので学問的誤りがあるかもしれませんが、学問の雰囲気を掴んでいただくことを趣旨としておりますので、どうぞ間違いには優しく目を瞑るか、そっと教えていただくよう、よろしくお願い致します。
さて、本記事は「数学・物理・情報を全部学べる」ことで有名な工学部計数工学科についてです!計数工学科3年、数理情報工学コース所属のKBお送りいたします。お楽しみあれ。
また、計数工学科の制度や学生生活は、UT-BASEの学部学科紹介ページをご覧ください。
数学、物理、情報
計数工学科は工学部応用物理系に属する近年人気急上昇中の学科です。その類稀なる学科名は「計測+数理」に由来し、工学的な応用を見据えて数理や物理を基礎から学ぶことができます。こういう説明をすると数学や物理が主のように聞こえますが、計数は昨今流行の「情報系」学科であると言っても問題はないでしょう。数理と物理は、情報の概念や技術と強く結びつきます。
ただここで一つ、根本的な疑問が浮かびます。数学や物理の内容は、多くの人にとって具体的なイメージがつきやすいでしょう。何行にもわたる積分計算をしたり、坂の上から球を転がしたりするあれらです。それと比べて、「情報」はどうでしょうか。思い浮かぶのはパソコンのキーボードくらいで、何とも曖昧な響きがします。
「情報」なる学問は一体何なのか。
「情報系に興味があるんだ」と語るあの人はつまり何がしたいのか。
ここでその問いに対する切れ味鋭い回答を出すことはできないかもしれません。「情報系」で学びうることはWebプログラミングから機械学習、ハードウェアの設計に通信技術と多岐にわたっています。一口に「これが情報の全てだ」と言うことはできません。
本文で扱いたいのは、「情報」という学問の「情報っぽい」ところです。隣のクラスの誰々が部活をやめたという噂話や、朝からテレビでやっているニュース番組の「情報」と、数理的な意味での「情報」は少し違います。情報を数学的に論じるというのはどういうことなのか、具体的な応用例を通じてその雰囲気を味わっていただくことで、「情報」という学問の便利さや面白さが少しでも伝わり、「情報」という漠然とした言葉の輪郭がわずかにでもくっきり見えるようになったら幸いです。
目次
#1 情報の価値
情報理論とは、情報を数理的に定義し、その価値や効率的な通信方法を論じる学問分野です。まず第1章では、情報の価値という抽象的なものはどう定量的に捉えればいいのかということを考えます。日常的な用法での「情報の価値」は、大いに主観をはらんでいそうですが、情報理論ではメッセージ自体の持つ意味には立ち入りません。では、何を基準に情報の価値の大小を決めれば良いのでしょうか。
ここで、「明日雨が降る」という情報の持つ重要性について考えてみます。同じ「明日雨が降る」という予報でも、それを聞く場所が熱帯雨林であるか砂漠であるかでだいぶ意味が変わってきます。毎日のように雨が降っている前者では「でしょうね」としか思いませんし、降雨が珍しい後者では驚きのニュースとなります。つまり、「明日雨が降る」という情報は、砂漠での方が客観的な価値が高い、というのが直感です。
そして、この「珍しいニュースほど大事である」という直感を反映するには、次のように情報の価値を定めれば良さそうです。
生じる確率の低いメッセージほど、情報の価値が高い。
つまり情報理論における情報の価値は、その生じる確率から決まります。その時期その場所で雨が降る確率だけが問題で、「明日は遠足だから」といった主観が入り込む余地がありません。
情報の価値を求める具体的な関数の形を決めるために、もう少し細かくみていきます。「明日は雨か雪である」という情報(価値X)を得た後に「明日は雪ではない」という情報(価値Y)を得るのと、「明日は雨である」という情報(価値Z)をいきなり得るのとでは、結果的に得た情報は全く同じなので、それぞれの合計も同じ(X+Y=Z)であってほしいです。
こういった加法性の要請を踏まえると、確率pで発せられるメッセージの価値は、以下のように決まります。
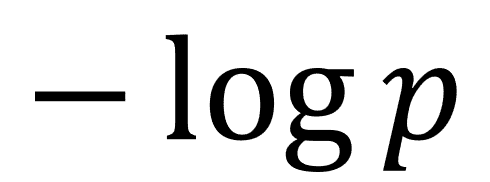
これを、メッセージがもつ情報量と言います。なお、対数の底は慣習的に2にとっています。
この情報量の関数から、次のことが分かります。すなわち、対数の加法性より、例えば1/2に絞る情報を聞いてからさらに1/2に絞る情報を聞くのと、一気に1/4に絞る情報を聞くのとで、情報量の和は等しくなります。
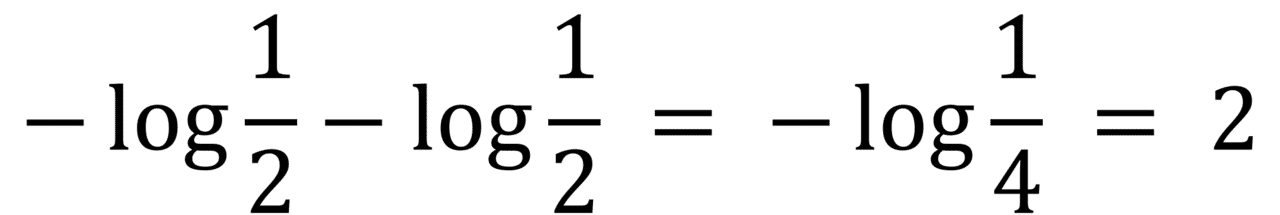
また、p <= 1より情報量が常に非負であること、そしてpが小さくなるほど大きくなることが確かめられます。
#2 「いい質問ですね」の程度
さて、メッセージ一つの価値(=情報量)が定義できたので、今度はメッセージ全体の持つ情報量について考えてみましょう。これは、実際に得られるメッセージの持つ情報量の期待値として定義されます。
例えば、天気予報の「明日は※※」(※※ = 晴 or 雨 or 曇り or 雪)のように発せられうるメッセージがn種類あり、それぞれの確率がp_1,p_2,...,p_n(合計は1)であったとしましょう。
p_1の確率で「情報1」が発せられ、そのとき-log_(p_1)の情報量が得られる、といった具合です。
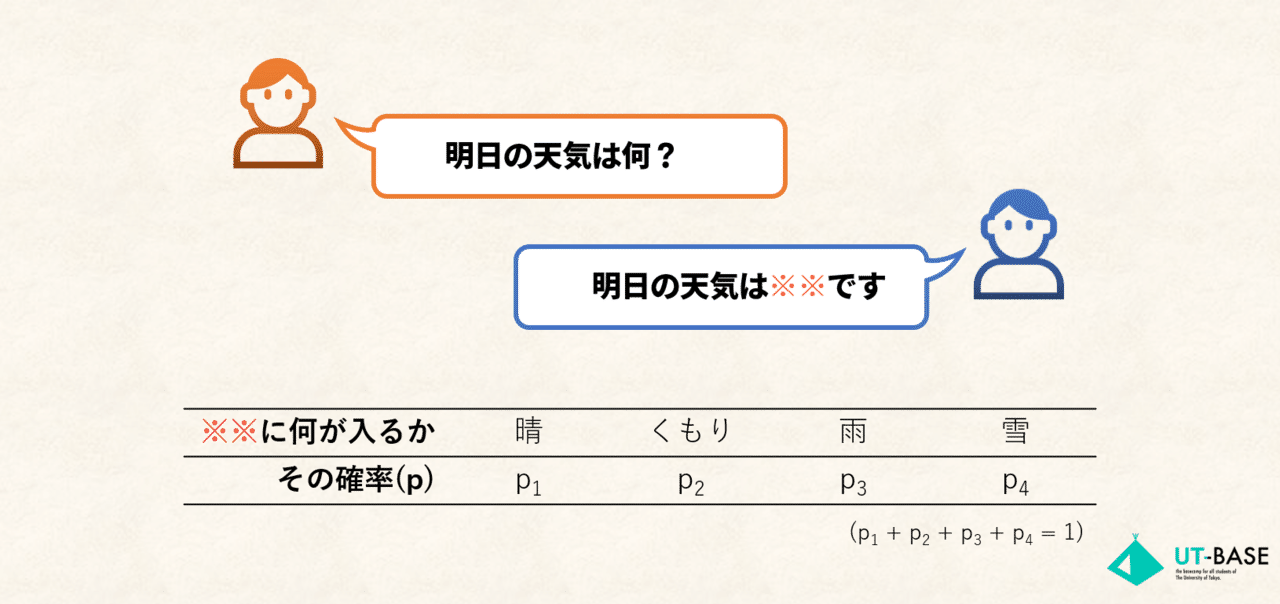
このとき得られる情報量の期待値(=平均情報量)は以下の通りです。
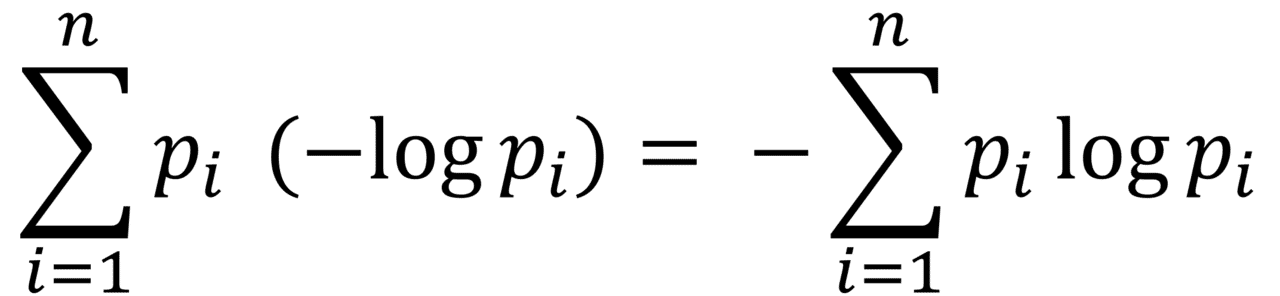
これは、p_1,p_2,...,p_nが満遍ない(全て1/nなど)ほど大きい値をとり、偏りが大きい(p_1だけ1など)ときは0に近づきます。つまり、平均情報量は情報の無秩序さ、不確実性の尺度であり、エントロピーとも呼ばれます。
この平均情報量の概念をより理解するために、次のような単純な数字当てゲームを考えましょう。
【ルール】
Aさんが頭の中に1から32までの整数を一つ思い浮かべ、
Bさんは「はい」か「いいえ」で答えられるような質問のみによってその数字に迫っていきます。
例えば、Aさんが12を思い浮かべているとして、「4の倍数ですか?」「はい」「20より小さいですか?」「はい」「10より小さいですか?」「いいえ」「12ですか?」「はい」という風にゲームは進行します。
このゲームにおいて、Bさんがとるべき最善の戦略を情報理論の観点から考えていきます。
例えば、いきなり「4の倍数ですか?」と問うのは得策でしょうか。仮に答えが「はい」であった場合、一気に候補は4分の1に絞れますが、「いいえ」であった場合は4分の3にしか絞れません。そして、「はい」という答えが返ってくる確率は1/4,「いいえ」という答えが返ってくる確率は3/4です。したがって、「4の倍数ですか?」という問いの返答を聞いて得られる情報量の期待値は-1/4log(1/4)-3/4log(3/4) です。
ではどんなときに得られる情報量の期待値が最大化するか(=「いい質問」か)というと、先述のように確率が一様分布の時、つまり、「はい」と「いいえ」がちょうど半々の確率で返ってくるような質問をした場合です。「偶数ですか?」「16以下ですか?」といった問いが、平均情報量を最大化する、情報理論的に「いい質問」なのです。これは直感的には、「答えが全く予想のつかない質問ほどする価値がある」と理解できます。
※参考までに、エントロピーの最大化問題を考えてみましょう。難しく感じる方は全力でスルーしてください。(画像はUT-BASE作成)
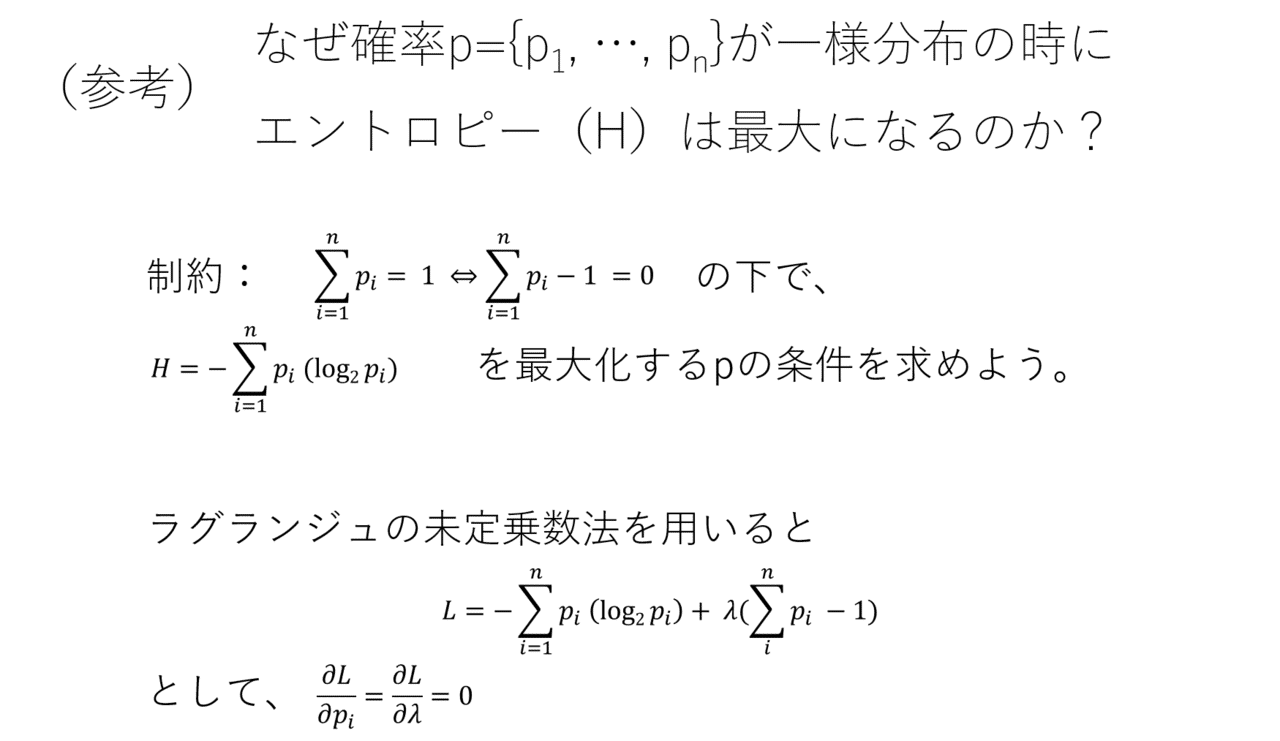
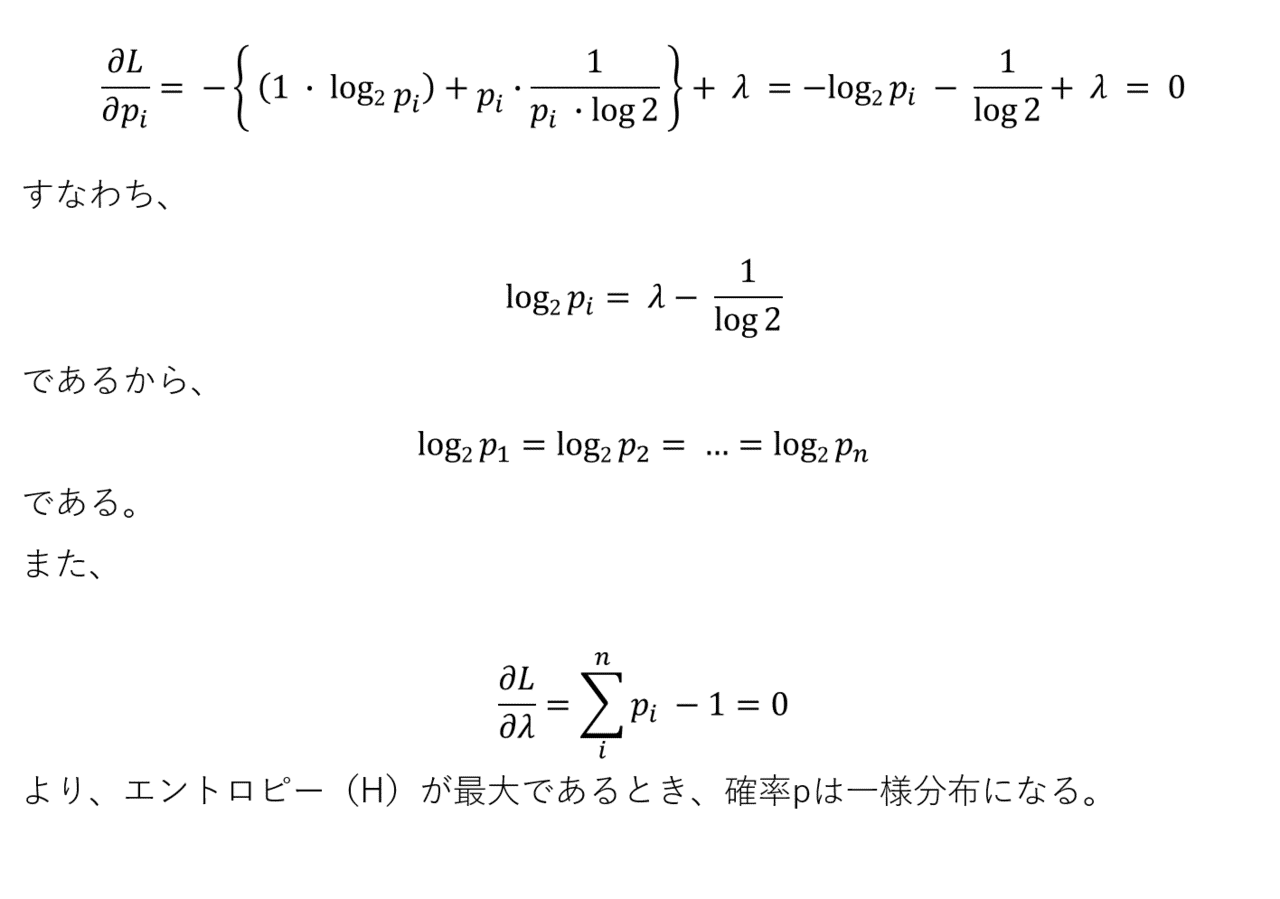
数当てゲームの話に戻ります。
結果的に、Bさんは常に「はいといいえが二分の一ずつの確率で返ってくる質問」をすればよく、
「16以下ですか?」 → 「はい」
「8以下ですか?」 → 「いいえ」
「12以下ですか?」 → 「はい」
「10以下ですか?」 → 「いいえ」
「11以下ですか?」 → 「いいえ」
と5つの質問をした段階で確実に「12」という答えに辿り着けます。これが、質問回数の期待値を最小にするという意味で最善の戦略です。
ただ、やっていることは毎回範囲を半分に絞っているというだけなので、二分探索と同じであり、今ひとつ平均情報量の計算の威力が実感できません。そこで最後に、この「平均情報量を最大化する」という方針に基づいて、より複雑なゲームに対する戦略を考えます。
#3ヌメロン最強AIを作る
「ヌメロン」という知る人ぞ知る推理ゲームがあります。これは、前述のものと比べ高度な数字当てゲームであり、ここでは以下のようなルールのものを考えます。
【ルール】
1. Aさんは各桁の数が相異なる4桁の自然数Xを一つ思い浮かべる。
2. Bさんは各桁の数が相異なる4桁の自然数Yをコールする。
3. AさんはXとYを見比べ、コールされた番号がどの程度合っているかを発表する。数字と桁が合っていた場合は「EAT」(イート)、数字は合っているが桁は合っていない場合は「BITE」(バイト)となる。(例として相手の番号が「1502」・コールされた番号が「1234」であった場合は、3桁のうち「1」は桁の位置が合致しているためEAT、「2」は数字自体は合っているが桁の位置が違うためBITE。EATが1つ・BITEが1つなので、「1EAT 1BITE」となる)
4. 4EATを相手に発表させる(=完全に当てる)まで2,3を繰り返す。
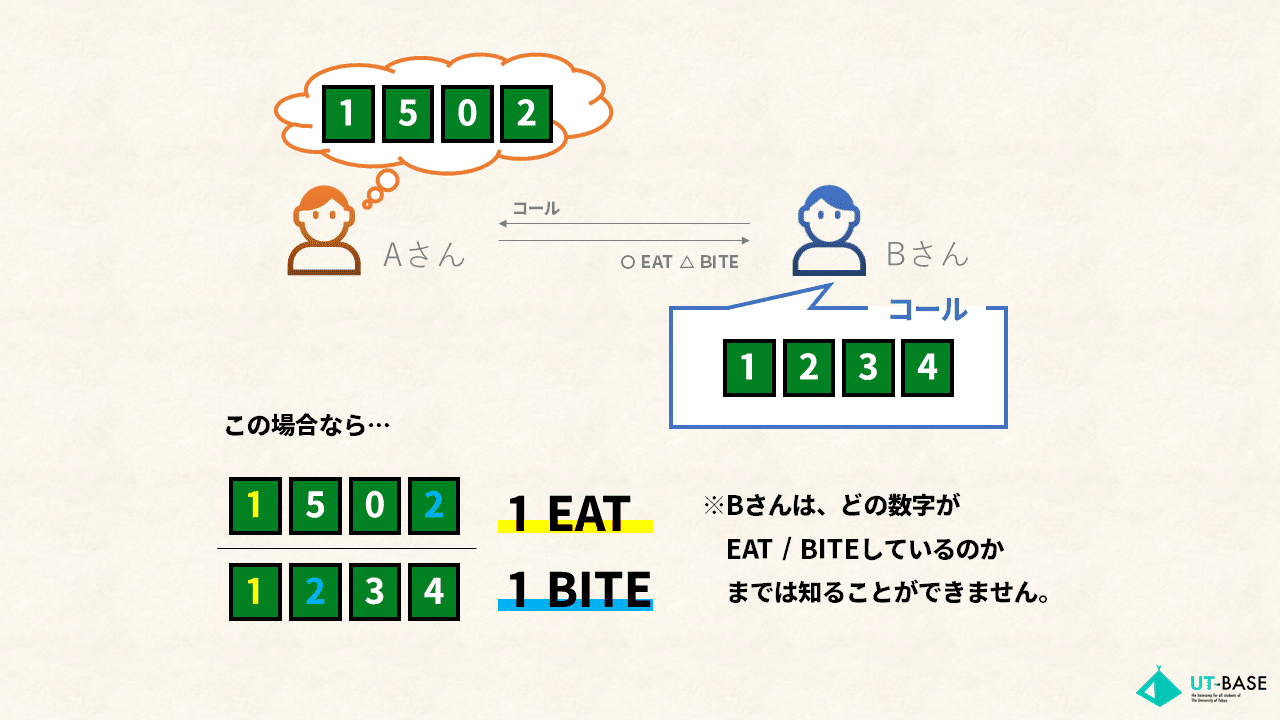
このゲームは本来、お互いに数字を思い浮かべ、先に当てた方が勝ちというゲームですが、今回は上のように単純化しました。
人間対人間でやる場合、どこが確定したか、次のどの数をコールすれば確定させることができるかなど考えるべきことがたくさんあり、非常にスリリングな頭脳ゲームとなります。
少し無粋ですが、このゲームでも最善の戦略を考えてみましょう。今回はコールに対する回答が「はい」「いいえ」の二択ではなく、「○EAT △BITE」という形で与えられるので前ほど単純には見えません。しかし、方針自体は一緒で、平均情報量を最大化するコールをすればいいのです。
まず、その時点でAさんが思い浮かべた自然数Xの候補として残っている数を求めておきます。これは、候補全体から、コールごとに、Aさんの発表と整合しない数を削っておけばよいです。
その上で、次にするコールとしてどれが有効かを、そのコールをしたときに得られる平均情報量を計算することで調べていきます。
可能なコール全てに対し、そのコールに対する返答が○EAT △BITEとなる確率を(残っているXの候補を参照して)それぞれ求め、最後にその確率分布のエントロピー(=平均情報量)を計算します。そうして、一番平均情報量が高くなるコールを採用すればよいのです。
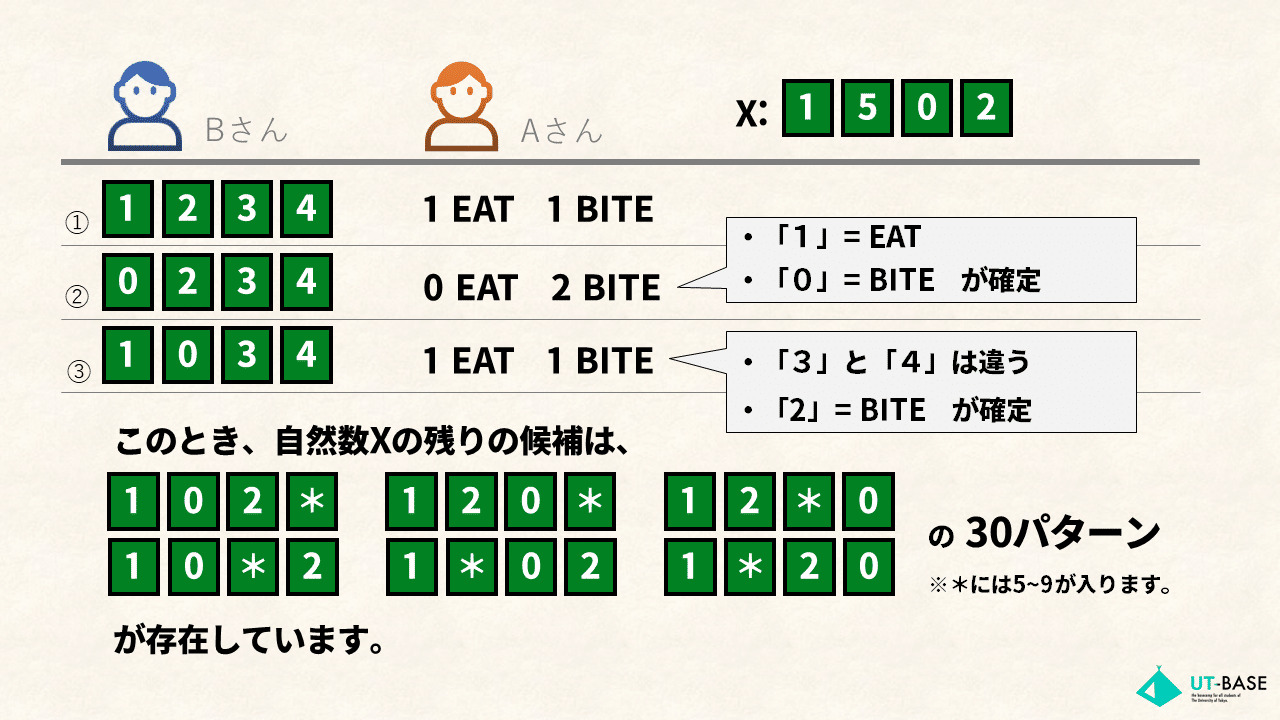
もっとも、このような全探索とlogの計算を含む力技を、人間が使うことはできません。そこで、これらの計算を実行して常に一番効率のいいコールをしてくるプログラムを作成しました。(コードは後掲)これを用いて実際に遊んでみると、以下のようになります。
【#5963を思い浮かべた】
7394
0 2
3578
0 2
9683
1 2
8901
1 0
6905
1 2
I am confident that your number is :
5963
4 0
I identified your number by 6 tries!
このように、魔法のような素早さで思い浮かべている数を当てられてしまいました。平均情報量という概念を取り入れただけなのに、まるで自分の頭の中を完全に読まれているかのような錯覚に陥ります。これこそ情報理論の威力であり、面白さだと言えるでしょう。
おわりに
難しい話が続きましたが、最後までお読みいただきありがとうございました。
本文で扱ったのは平均情報量を利用したゲームの戦略であり、一応は完全な答えが出るようなものでしたが、もっと多くのファクターを考慮に入れて手法を改善する余地があります。
例えば、ここでは相手がどの数字を選ぶかについては同様に確からしいことを(暗に)仮定していましたが、実際に人間が数字を選ぶときには偏りがあると思われます(1234、9753などの規則的な並びは選びづらい、など)。
それならば、対戦データをたくさん集めて統計的な分析を行い、思い浮かべる数の事前分布を得ることで、より有効な選択ができるかもしれません。
また、桁数が大きい場合、全探索を行うには計算量が大きくなりすぎてしまいます。そこで、効率よく探索を行う最適化アルゴリズムが使える可能性があります。こういったことも全て数理情報の範疇であり、計数工学科で学べることです。
さらに、数理の応用先は、ゲームのようにルールがきっちり決まったものに止まりません。現実世界の様々な問題は、数理的にモデル化し、代数・算法・幾何・確率・解析の手法を適用することで解明・解決に導くことができ、プログラミングや計算機がそのための具体的な手段となります。
本文はあくまで「情報」の「情報っぽさ」に焦点を当てましたが、計数工学科で扱う理論や手法は多岐にわたっています。今回の話に興味を引かれた方、数理の応用をもっと知りたいという方は、ぜひ計数工学科への進学を検討してはいかがでしょうか?










